Blaise Pascal (Clermont-Ferrand, 19 juni 1623)

was een buitengewoon begaafde Franse wis- en natuurkundige, christelijk filosoof, theoloog en apologeet.
Alhoewel Pascal tot de rooms-katholieke Kerk behoorde, was en is hij ook van grote invloed op het protestantisme.
Zijn belangrijkste prestaties zijn:
hij legde de grondslag voor de waarschijnlijkheidsrekening (samen met Fermat, die van mening was dat Pascal
willekeurig welk wiskundig probleem zou kunnen oplossen).
Pascal legde eveneens de basis voor de integraalleer en gaf betekenis aan het begrip oneindigheid.
hij bouwde een van de eerste mechanische rekenmachines (optelling en aftrekking) (1642).

De driehoek van Pascal is een rangschikking van de binomiaalcoëfficiënten
in rijen voor toenemende n beginnend met n=0 en op elke rij de n+1 binomiaalcoëfficiënten
voor de mogelijke waarden van k.
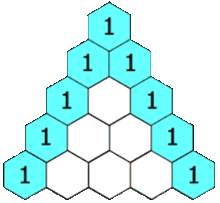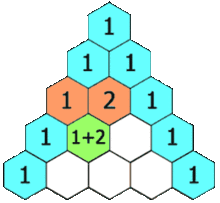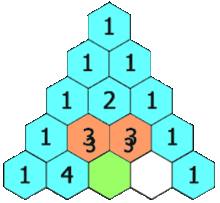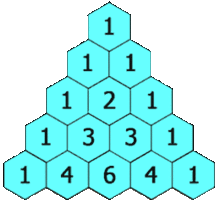
In de driehoek komt de eigenschap tot uitdrukking dat elke binomiaalcoëfficiënt de som is
van de twee bovenliggende. De getallen in de driehoek geven het aantal wegen aan vanaf de top
naar de plaats van zo'n getal, waarmee ook de besproken eigenschap verklaard is.
Omdat er steeds 2 keuzen zijn om de weg naar onder te vervolgen is de som van de getallen op
een rij de overeenkomstige macht van 2.


De driehoek van Pascal heeft vele eigenschappen:

de som van rij n is gelijk aan 2n
de getallen op een rij vormen de coëfficiënten van de uitgeschreven uitdrukkingen voor (x + y)n
Als het element k = 1 uit een rij een priemgetal is, dan zijn alle nummers uit die rij
(behalve de 1 aan het begin en eind) deelbaar door dit getal. Voorbeeld: 1 7 21 35 35 21 7 1
Door de oneven getallen weer te geven als een zwarte punt ontstaat er een figuur met een fractale structuur,
de zogenaamde Sierpinski-driehoek.
Het aantal elementen in de onderstaande driehoeken wordt gegeven door de elementen (n,2) van de driehoek.