De Zeef van Eratosthenes (bibliothecaris van Alexandrië vanaf ca. 240 v.Chr.) is een al zeer lang bekend algoritme
om priemgetallen te vinden. Deze elegante methode is vooral efficiënt wanneer hij wordt gebruikt voor de kleinere priemgetallen.
De methode vergt echter het bijhouden van alle getallen kleiner dan de gebruikte bovengrens, wat naarmate de te bepalen
priemgetallen groter worden een steeds groter nadeel wordt.

Methode1.
Maak een gesorteerde lijst van alle getallen van 2 tot een zelf te kiezen maximum.
2.Kies het kleinste getal uit de lijst.
3.Streep alle veelvouden van het gekozen getal door (maar niet het getal zelf).
4.Kies het volgende getal uit de lijst en ga verder met stap 3.
De getallen die op deze manier overblijven zijn alle priemgetallen tot het maximum.

De procedure kan op enkele manieren versneld worden.

Het heeft geen zin in stap 4 een getal te kiezen dat al doorgestreept is, want alle veelvouden daarvan zijn al doorgestreept.
Men kan met doorstrepen beginnen met het kwadraat van het gekozen getal. Alle kleinere veelvouden zijn al doorgestreept.
Is het gekozen getal groter dan de wortel uit het maximum, dan is de procedure voltooid.


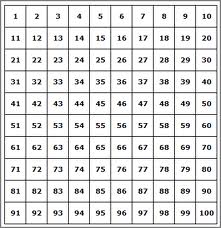
Priemgetallen (hele grote) liggen aan de basis van de Cryptografie
zoals gebruikt bij het verzenden van berichten over het internet.